Unlocking AES Encryption: A Deep Dive Into Its Inner Workings for Secure Data Protection

This article provides a comprehensive explanation of AES encryption, a robust method used to secure sensitive data. We delve into the intricate details of AES.

In an increasingly digital world, the security of our information has become paramount. Whether we are sending sensitive emails, conducting financial transactions online, or storing confidential documents, the need to protect our data from prying eyes has never been more critical. Encryption stands as the stalwart guardian of our digital privacy, serving as an impenetrable shield that keeps our information safe from unauthorized access.

In this article, we delve into the world of encryption, exploring its basic types — Symmetric and Asymmetric — and highlighting the key differences between them. Furthermore, we'll guide you on how to choose between these encryption methods by outlining scenario-specific use cases for each, enabling you to make informed decisions to safeguard your valuable data. We will also see in detail how the actual encryption and decryption take solace. Let's embark on a journey to unravel the secrets of AES encryption and enhance our understanding of digital security.

What Is Encryption?

Encryption is a fundamental technique in the realm of cybersecurity that involves converting plain, readable data into a coded or scrambled format, known as ciphertext, to protect it from unauthorized access during transmission or storage. It essentially transforms information into an unintelligible form, rendering it secure until it is decrypted back into its original state by an authorized party with the appropriate decryption key.

There are two basic types of encryption: Symmetric Encryption and Asymmetric Encryption, each with its own unique characteristics and use cases.

Symmetric Encryption

Symmetric encryption, also known as single-key encryption or private-key encryption, employs a single secret key for both the encryption and decryption processes.
In this method, the same key is used to both scramble (encrypt) and unscramble (decrypt) the data. Because of this, it is crucial to keep the key secret and securely share it only with trusted parties.
Symmetric encryption is typically faster and more efficient than asymmetric encryption, making it well-suited for encrypting large amounts of data, such as files and communications.
It is commonly used for securing the confidentiality and integrity of data at rest, like encrypting files on a hard drive, or for securing data in transit, such as encrypting network communications, audit logs, and transaction history.
Notable symmetric encryption algorithms include the Advanced Encryption Standard (AES), DES (Data Encryption Standard), and 3DES (Triple Data Encryption Standard).

Asymmetric Encryption

Asymmetric encryption also referred to as public-key encryption, uses a pair of mathematically related keys: a public key for encryption and a private key for decryption.
Unlike symmetric encryption, where the same key is used for both encryption and decryption, asymmetric encryption allows anyone to encrypt data using the recipient's public key, but only the recipient possessing the corresponding private key can decrypt and access the original data.
This method is highly secure and eliminates the need for a secure key exchange process, as the public keys can be freely shared.
Asymmetric encryption is commonly used for secure communications, digital signatures, and key distribution in secure systems.
Prominent asymmetric encryption algorithms include RSA (Rivest-Shamir-Adleman) and ECC (Elliptic Curve Cryptography).

This article will mainly focus on Symmetric Encryption.

Here's a detailed explanation of how symmetric encryption works:

Key Generation

The process begins with the generation of a secret key, which is a random or pseudorandom (generation of numbers or sequences that appear to be random but are actually generated by a deterministic process) sequence of bits. The key is typically a fixed length, such as 128 bits, 192 bits, or 256 bits, depending on the chosen encryption algorithm.

The strength of symmetric encryption largely depends on the length and complexity of this secret key. Longer keys generally provide stronger security but may require more computational resources.

We can generate the key in C# using the following code:

using System;

using System.IO;

using System.Security.Cryptography;

using System.Text;

public class HelloWorld

    public static void Main(string[] args)

        byte[] aesKey = GenerateAes256Key();

        // Print the AES key in Base64 format

        string base64Key = Convert.ToBase64String(aesKey);

        Console.WriteLine("AES Key (256 bits, Base64): " + base64Key);

    static byte[] GenerateAes256Key()

        using (Aes aesAlg = Aes.Create())

            aesAlg.KeySize = 256; // Set key size to 256 bits

            aesAlg.GenerateKey(); // Generate a random key

            return aesAlg.Key;

Encryption Process

When you want to encrypt a piece of data (plaintext), you use the secret key along with a symmetric encryption algorithm (e.g., AES) to transform the plaintext into ciphertext.

The encryption process involves several rounds of mathematical operations, such as substitution, permutation, and bitwise operations, that are applied to blocks of data. The secret key determines how these operations are carried out.

Few Keynotes

1. AES operates on fixed-size data blocks of 128 bits (16 bytes). This block size is a fundamental characteristic of the AES encryption algorithm, and it does not change.

2. AES can be used in different modes (e.g., ECB, CBC) that may require additional bytes for padding and initialization vectors (we will cover initialization vectors later in this article).

Let’s understand this process with an example. Considering we have the text “The password 486 must be kept safely somewhere,” we would like to encrypt it using the AES algorithm using a key with a size of 256 bits.

Here is how the total blocks are calculated:

The text contains 47 characters, including spaces and punctuation.

Each character in the text can be represented as a single byte (assuming standard character encoding like UTF-8).

Therefore, the text consists of 47 bytes.

You can use online tools like this one to know the total bytes of the text.

However, AES encryption processes data in blocks (chunks) of 16 bytes. Since the text is 47 bytes, it's not a multiple of 16, so padding would typically be added to make it a complete block. In this case, the padding would add 1 byte (to reach a total of 48 bytes as 16 X 3 = 48) to make it compatible with AES encryption.

Once we have decided on the block size (3 in our case), the next step would be to encrypt using the key.

Step 1: Initialization

Plaintext: "The password 486 must be kept safely somewhere."

Key: A 256-bit (16-byte) symmetric key (for simplicity, let's assume the key is "2B7E151628AED2A6").

Step 2: Key Expansion

The initial key "2B7E151628AED2A6" is expanded into a set of round keys. These round keys will be used in each round of encryption and are derived from the original key using a key expansion algorithm. Basically, the number of rounds depends on the length and complexity of your key.

Step 3: Rounds (Round 1 to Round 10)

In each round, four main operations are performed: SubBytes, ShiftRows, MixColumns, and AddRoundKey.

Round 1

a. SubBytes

Each byte of the plaintext is substituted using an S-box lookup table. For example, 'T' might be substituted with '8A', 'h' with '37', 'e' with 'D4', etc. This substitution adds confusion.

So after first round, our text might look like “8A37D499R9Z8ssC5I7rd9948699must99bD499kD4R9t99YWZ8fD4lY699sI7mD4C437D4K7D4.”

At this stage, it’s just like encoded text.

b. ShiftRows

Remember that AES encryption processes data in blocks (chunks) of 16 bytes. Consider it as a 4X4 matrix for one of the block:

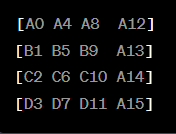
In the ShiftRows step, each row of the state matrix is shifted to the left by a certain number of bytes. The number of bytes shifted is determined by the row index.

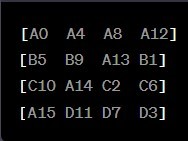
Row 0 (top row): No bytes are shifted. (same as original row) ShiftRows

Row 1: Shift one byte to the left. (B5 will be moved to left by 1 byte and so on for B9, A13)

Row 2: Shift two bytes to the left. (C10 will become the first element after shifting 2 bytes.)

Row 3: Shift three bytes to the left. (A15 will become the first element after shifting 2 bytes).

Resulting state:

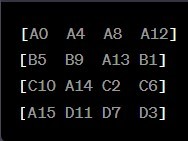
c. MixColumns

This involves mixing the columns of the data matrix (state) to further diffuse and spread the effects of encryption. The state is represented as a 4x4 matrix of bytes, and the MixColumns operation is applied to each column of this matrix.

Here's a breakdown of how the MixColumns operation works with respect to the columns in the state matrix:

Initial State (4x4 Matrix):

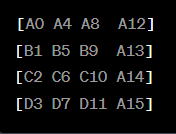
In the MixColumns step, each column of the state matrix is transformed by matrix multiplication with a fixed matrix (a predefined mathematical matrix). This multiplication is performed using finite field arithmetic (also known as Galois field arithmetic).

The multiplication of each column by this fixed matrix involves combining and altering the values in the column, resulting in a new column of bytes. This mixing operation introduces diffusion and further obscures the relationship between the input and output.

Resulting State:

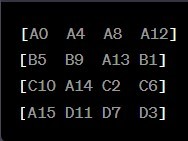
The red dot indicates a change in values.

d. AddRoundKey

The round key for Round 1 is XORed with the data. For example, the first 16 bytes of the key ("2B7E151628AED2A6") are XORed with the first 16 bytes of the plaintext.

f. Apply Initialization Vectors (IVs)

Normally, the IV is applied in the first round. Think of IV as an extra secret key to your encryption. if you send the same message multiple times, it might end up looking the same way every time without IV, and someone spying on your messages could figure out what's inside. So, when you send a message, you pick a random IV, mix it with your message, and then use AES encryption to scramble everything together. Because the IV is different each time, even if you send the same message, it will look completely different when scrambled.

Round 2 to Round 10

The same operations (SubBytes, ShiftRows, MixColumns, and AddRoundKey) are performed in each round using the appropriate round key.

Final Round

The final round is similar to the previous rounds but lacks the MixColumns step.

Step 4: Ciphertext Output

After completing all rounds, you have the ciphertext. It's the result of the final AddRoundKey operation.

Now, the "The password 486 must be kept safely somewhere." plaintext has been encrypted using the AES algorithm with the provided key. The resulting ciphertext will appear as a seemingly random set of bytes. Decrypting it without knowing the key would be computationally infeasible, providing the data confidentiality that AES encryption offers.

Please note that this is a simplified explanation, and in a real-world scenario, AES encryption involves more complex mathematical operations and uses larger data blocks. However, this example should give you a basic understanding of the AES encryption process.

Decryption Process

To decrypt the ciphertext and recover the original plaintext, you use the same secret key and the symmetric encryption algorithm in reverse, effectively undoing the transformation and yielding the original plaintext.

Here is an example of encryption and decryption code in C#:

using System;

using System.IO;

using System.Security.Cryptography;

using System.Text;

class Program

    static void Main()

        // The text to be encrypted

        string plaintext = "Hello, World!";

        Console.WriteLine("Original Text: " + plaintext);

        // Encrypt the text

        string ciphertext = EncryptText(plaintext, "KeyGenereatedFromGenerateKeyFunction");

        Console.WriteLine("Encrypted Text: " + ciphertext);

        // Decrypt the text

        string decryptedText = DecryptText(ciphertext, "KeyGenereatedFromGenerateKeyFunction");

        Console.WriteLine("Decrypted Text: " + decryptedText);

    static string EncryptText(string plaintext, string base64Key)

        byte[] key = Convert.FromBase64String(base64Key); // Convert key from Base64 to byte array

        using (Aes aesAlg = Aes.Create())

            aesAlg.Key = key;

            aesAlg.GenerateIV(); // Generate a random IV

            using (MemoryStream msEncrypt = new MemoryStream())

                using (CryptoStream csEncrypt = new CryptoStream(msEncrypt, aesAlg.CreateEncryptor(), CryptoStreamMode.Write))

                    using (StreamWriter swEncrypt = new StreamWriter(csEncrypt))

                        swEncrypt.Write(plaintext);

                byte[] iv = aesAlg.IV;

                byte[] encryptedBytes = msEncrypt.ToArray();

                // Combine IV and encrypted data into a single byte array

                byte[] result = new byte[iv.Length + encryptedBytes.Length];

                Array.Copy(iv, result, iv.Length);

                Array.Copy(encryptedBytes, 0, result, iv.Length, encryptedBytes.Length);

                return Convert.ToBase64String(result);

    static string DecryptText(string ciphertext, string base64Key)

        byte[] key = Convert.FromBase64String(base64Key); // Convert key from Base64 to byte array

        byte[] inputBytes = Convert.FromBase64String(ciphertext);

        byte[] iv = new byte[16]; // AES IV size is always 16 bytes

        // Extract IV from the input bytes

        Array.Copy(inputBytes, iv, iv.Length);

        using (Aes aesAlg = Aes.Create())

            aesAlg.Key = key;

            aesAlg.IV = iv;

            using (MemoryStream msDecrypt = new MemoryStream())

                using (CryptoStream csDecrypt = new CryptoStream(msDecrypt, aesAlg.CreateDecryptor(), CryptoStreamMode.Write))

                    // Decrypt the ciphertext (excluding the IV)

                    csDecrypt.Write(inputBytes, iv.Length, inputBytes.Length - iv.Length);

                // Get the decrypted bytes

                byte[] decryptedBytes = msDecrypt.ToArray();

                // Convert the decrypted bytes to a string

                string decryptedText = Encoding.UTF8.GetString(decryptedBytes);

                return decryptedText;

Tip: You can use online tools like: this one to test the code online.

Key Management

One of the critical aspects of symmetric encryption is key management. Since the same key is used for both encryption and decryption, it is crucial to keep the key secret and protect it from unauthorized access.

Key management includes securely generating, storing, and sharing the secret key with authorized parties. Any compromise of the key can lead to the compromise of encrypted data.

Current industry standards include storing the key in a vault over the cloud using Azure Vault or Amazon AWS Secret Manager. The other approach is to store the key value as an environment variable on the server running the encryption/decryption. I will not recommend storing the key in some configuration files like web.config due to security reasons.

Conclusion

In this article, we explored what AES encryption is and how the encryption/decryption works in detail. The algorithm has been adopted by the U.S. Government as it supersedes other available algorithms. Nowadays, most of the system requires secure transfer of data, and AES is the de facto standard when it comes to cybersecurity.

We Provide consulting, implementation, and management services on DevOps, DevSecOps, DataOps, Cloud, Automated Ops, Microservices, Infrastructure, and Security

Services offered by us: https://www.zippyops.com/services

Our Products: https://www.zippyops.com/products

Our Solutions: https://www.zippyops.com/solutions

For Demo, videos check out YouTube Playlist: https://www.youtube.com/watch?v=4FYvPooN_Tg&list=PLCJ3JpanNyCfXlHahZhYgJH9-rV6ouPro

If this seems interesting, please email us at [email protected] for a call.